A few weeks ago, Dan Banquer of R.E. Designs forwarded me a very interesting AES paper entitled "0dBFS+ Levels in Digital Mastering" by Soren H. Nielsen and Thomas Lund of T.C. Electronic A/S.
Essentially, this paper explains why playing back a digital recording (by "reconstructing" the Nyquist bandwidth-limited analog waveform through a digital-to-analog converter and applying an appropriate reconstruction filter) will result in peaks that are higher in amplitude than the highest digital sample captured on the recording.
To put it in simpler terms, when you make a digital recording, an analog waveform (represented by an electrical signal with a continuously varying voltage) is sampled at regular intervals and converted to a set of numbers. Each number, or digital sample , correspond the voltage of the electrical signal at a specific point in time. These numbers are stored in binary form with a specific word size (typically 16-24 bits). The minimum and maximum numbers that can be stored depends on the word size, and corresponds to the voltage range of the electrical signal. For example, the maximum digital sample in a 16-bit recording is 32,767 and this is also referred to as 0dBFS (0dB "full scale").
When this recording is played back, a digital to analog converter converts these binary values back to a set of voltages, and a reconstruction filter is applied to convert these voltages back into a continuous signal. It is possible for the reconstructed analog waveform to have voltages that are higher than the highest digital sample recorded. So, if the highest digital sample captured happens to correspond exactly to 0dBFS, the recording, when played back, may result in an analog waveform exceeding 0dBFS. The subsequent analog stage of the playback chain may not be capable of handling a signal greater than 0dBFS (also known as "0DBFS+"), resulting in clipping distortion.
"What the ...?" I hear you say. "How is that possible?"
It has all to do with inter-sample peaks. If you record a sine wave at frequencies near integer fractions of fs (where fs = "sampling frequency"), such as fs /4 and fs /2, then (depending on the phase of the sine wave with respect to the sampling times), the digital samples may never actually capture the true peak of the analog waveform. Hence, when this recording is reconstructed back into analog, it will result in analog peaks higher than the highest digital sample captured.
A "raw" recording - captured directly from an analog to digital converter (ADC) with no subsequent digital signal processing, should NEVER contain 0dBFS+ levels. This is because the original analog waveform should always be below 0dBFS, provided the recording gain is set correctly. However, subsequent processing of this recording may create 0dBFS+ inter-sample peaks. For example, "normalization" is a common technique - this multiplies every digital sample by a constant value so that the highest digital sample captured becomes 0dBFS. This will cause any inter-sample peaks that exceed the highest digital sample captured to exceed 0dBFS.
Read "The Case for NOT Going Above 0dBFS in Digital Playback Systems" for more information on this topic.
Here is an example: a 0dBFS 11,025Hz sine wave ( fs /2) is "digitally synthesized" at 44.1kHz/16-bits, with a phase of 45° with respect to the sampling boundaries. The highest digital samples are captured at -3dBFS (because the 0dBFS peaks of the sine waves are always in between samples). If the digital samples are "normalized" (by multiplying each sample by 3dB) then the highest digital samples are now at 0dBFS, but when played back will result in a reconstructed sine wave with peaks at +3dBFS.
This is illustrated by the following diagram. The left channel has been normalized so that the highest digital samples are at 0dBFS, and the right channel is -6dB lower in level for comparison purposes. As you can see, the reconstructed analog waveform will actually peak at +3dB FS on the left channel and -3dBFS on the right channel (in between the digital samples, represented by tiny green squares):
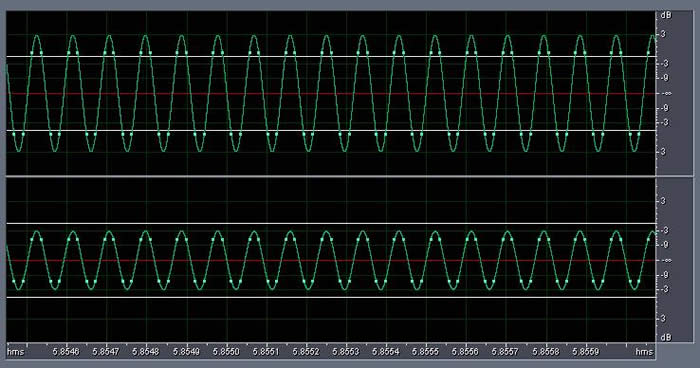
So you can imagine, if this waveform is played back on a CD player, the analog circuit in the CD player better be able to handle a signal at +3dBFS!
The authors of the AES paper (Søren H. Nielsen and Thomas Lund) then conducted measurements of several CD players using test signals specifically designed to illustrate 0dbFS+ levels, and concluded that NONE of the players sampled were able to deal with 0dbFS+ levels without distortion.
Yes, but what does it mean for me?
I was intrigued to find out how my system would handle 0dBFS+ levels, particularly my various players and the D/A conversion built in my amplifier.
I reconstructed the test signals mentioned in the paper, and burnt a music CD containing those test signals. I then played that CD on my system in various ways, and recorded the results using the Audiotrak Prodigy 7.1 soundcard in my HTPC at 96kHz/24-bits. I then analyzed the recorded signals for any signs of distortion.
I created the following sine waves as per the paper entirely in the digital domain as 30 second wave files at 44.1kHz/16 bits ( fs ):
- Sine wave @ 997Hz 0° phase (reference for distortion tests)
- Sine wave @ 5,512.5Hz 90° phase ( fs /8)
- Sine wave @ 5,512.5Hz 67° phase ( fs /8)
- Sine wave @ 7,350Hz 90° phase ( fs /4)
- Sine wave @ 7,350Hz 60° phase ( fs /4)
- Sine wave @ 11,025Hz 90° phase ( fs /2)
- Sine wave @ 11,025Hz 45° phase ( fs /2)
All signals were normalized to 0dB FS on the left channel, and -6dB FS on the right channel.
I also generated the following sine waves, also entirely in the digital domain as 30 second wave files at 44.1kHz/16 bits ( fs ):
- Sine wave @ 5,512.5Hz ( fs /8)
- Sine wave @ 7,350Hz ( fs /4)
- Sine wave @ 7,350Hz ( fs /4)
- Sine wave @ 11,025Hz ( fs /2)
The only test signal mentioned in the article that I was not able to generate is the pseudo-random sequence consisting only of +1 and -1 values repeating every 32767 samples.
I played back the CD in the following players/configurations (all via the analog pre-amp section of my Denon AVC-A1SE+ amplifier - this is so that we are measuring the "system"'s response to 0dBFS+ levels and not just the players' ability to reproduce them):
- Sony SCD-XA777ES, analog outputs
- Denon DVD-2200, analog outputs
- Denon DVD-2200, digital outputs via the D/A stage of the Denon AVC-A1SE+ (in AL24+ mode)
- Panasonic DVD-RP82, analog outputs, no upsampling
- Panasonic DVD-RP82, analog outputs, upsampling algorithm 1 (Remaster 1)